In the wake of the recent global health threat from the novel coronavirus, the World Health Organization (WHO) issued immediate counter-measures to control the spread of the disease. Have you wondered how experts gain insights that lead to timely decisions? Or how they arrive at estimates of the number of people who might get infected? How do experts visualise the progress of the infection and its capacity to cross borders? Based on what conclusions, are lockdown directives issued? And finally, how can experts predict how long an epidemic will last?

The answer lies in maths. Mathematical functions can be applied as tools to describe the dynamics of how infectious diseases propagate among people. Mathematical Modelling generates a picture or a ​‘model’ of the dynamics of the disease, which can be visually represented by graphs, charts and comparative tables. 

Models provide valuable inputs to visualise how diseases affect people. Hence, epidemiologists — public health experts – use them extensively to assess risk or to analyse intervention strategies to control or prevent diseases. Insights available from models facilitate disease management protocols like mass vaccination drives, treatment patterns, and precautionary procedures. 

When the infectious disease is an unknown one, such as the present coronavirus pandemic, models become all the more vital for policymaking. ​“Models can help answer several questions that impact policy. In most cases, they are the only rational way of formulating such questions and evaluating how different interventions might shape the spread of the disease,” says Gautam I Menon, Professor, Departments of Physics and Biology, Ashoka University (Sonipat) and Institute of Mathematical Sciences (Chennai).

The hidden patterns

Mathematical models have century-old roots. In the 1920s, William O Kermack and AG McKendrick observed that a population that is exposed to an infection can be divided into three categories– Susceptible, Infected, and Recovered. They found a way of representing the numbers in each of these groups mathematically. 

They translated their idea into differential equations, which draw a relationship between a physical quantity and its rate of change. The Kermack-McKendrick equation estimates what fraction of the population, over time, enters into one or the other of these categories, starting from an initial state in which one infectious person ​‘seeds’ the infection among the rest. 

From this, Kermack and McKendrick devised their classic SIR (Susceptible-Infected-Recovered) model that could predict disease spread. Since then, mathematical models have played a prominent role in transforming public health care. Governments, health organisations, scientists and hospitals depend heavily on models to deal with the onslaught of issues that arise out of medical problems.

“Virtually all other models in use today build on the intuition of the SIR model but often introduce additional categories,” says Menon. 

Compartments, Networks and Agents

Several factors govern the transmissibility of the infection from the affected to the unaffected. The spread can be through direct contact or through water, air, or surfaces which harbour the pathogen. Also, disease dynamics can be studied at different scales: the single individual, small groups of people, and among entire populations. Different models are chosen based on the complexity of available data. In their modern avatar, models are simulated by computers that generate the numbers and distribution patterns of infections. 

In the simple SIR model, people fall under any of the three ​‘compartments’ – Susceptible, Infected, or Recovered. The equations describing them assume that the Infected can interact with the Susceptible, infecting them and converting them into Infected as well. As the Infected increase, the Susceptible decline. Infected people can also recover, and are then assigned to the Recovered compartment.

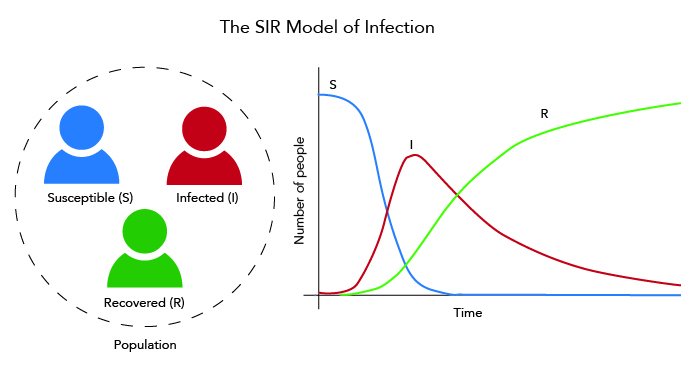
These equations can then be solved to understand how the number of infected people changes with time. Sometimes, additional categories are introduced to the basic model. For example, an infected person who is not displaying any symptoms can form a new category. Sometimes, additional factors such as age also need to be taken into consideration.

But reality presents many additional degrees of complexity. People mix randomly and socialise, which has a marked effect on disease propagation. Crucial aspects such as infection progression, the degree of susceptibility of the person, or demographic factors are left out in the basic model, calling for more comprehensive models.

Some diseases (such as measles or sexually transmitted diseases) spread quickly due to social or physical interaction among people. A network model takes these additional aspects into consideration. Here, the individuals are the ​‘nodes’ while their interactions form the ​‘links’ of a network. ​“For example, members of close-knit families, teachers and their students, or doctors and their patients are linked through some physical proximity that can propagate the disease, forming well-networked people with many links,” explains Menon.

People mix randomly across geographies as well, resulting in the disease crossing borders. Demographic differences, social influences, and predispositions also influence disease propagation. Some of this diversity can be simulated using a computer program and checking for the probable outcomes when the many variables interact with each other. 

Such variables can be incorporated into an agent-based model that allows researchers to analyse patterns of epidemic spread in these more complex situations, which can then be compared to the observed data. By incorporating factors that describe how an individual responds to interaction, environment, place, and time, the model estimates the probable spatial distribution of the disease and its evolution in time. 

In the agent-based model, each individual is an ​‘agent’ defined by particular attributes. For example, an agent might be at different geographical locations, e.g. work or home. Then a computer program is used to simulate the interactions of the agents and the spread of disease among agents. This model offers flexibility in deciding what goes into the definition of an agent and the way agents transfer diseases among themselves. ​“For example, each agent could have a different immune response to the disease, or the age of the agent could be relevant,” elaborates Menon. He also points out that such intricate modelling needs high-power computers to perform the number crunching.

Impacting policies

Such systematic processes for estimation of variables and parameters inherent to an epidemic proved invaluable in the case of the present coronavirus outbreak. Several models have emerged, uncovering the transmissibility and the destructive patterns of the pathogen. ​“One model used airline traffic data to find out how the infection might have spread to other regions outside Wuhan (the epicentre of the disease in China),” says Menon. 

Such models can calculate the expected number of cases and how quickly the disease might spread, along with helping quantify quarantining and social distancing measures. They aid health services in budgeting medical equipment and facilities like ICU beds and ventilators, facilitating immediate policymaking.

“Although a comprehensive model specific to India is yet to emerge, the Indian government seems to be following most of the WHO guidelines carefully and constantly reassessing its response,” says Menon. He emphasises that social distancing is one way of controlling disease spread by changing the way people interact with each other. By exercising a collective responsibility in implementing the measures, we can avoid overwhelming the medical services or clogging them, he concludes.